What does it mean to "own" a bitcoin?

Many people have heard of Bitcoin, a digital currency that does not require a specific government issue, and does not rely on banks to manage accounts and verify transactions. No one even knows its inventors. Many people don’t know the above. The answer to that question, or at least not fully understood. To understand, and to make the technical details behind Bitcoin intuitive, we will clarify step by step from how you will invent Bitcoin.

First we start with the public ledger you use to record your dealings with your friends, but your mutual trust with your friends and the rest of the world is beginning to diminish. But smart you introduce some concepts in cryptography to solve the crisis of trust. , you have created a new thing called "cryptocurrency".
Bitcoin is just the first example of a widely used cryptocurrency, and today there are more cryptocurrencies that can be traded with traditional currencies. Now you can help us understand if you want to invent your own cryptocurrency. Nowadays, the theoretical basis of several major cryptocurrencies, there are different design spaces in different aspects behind it.

In fact, I chose this topic because I have a lot of attention, capital investment, and even honest media over the past year. I don’t comment on the current and future exchange rates, but I Anyone who wants to buy cryptocurrencies should understand what the cryptocurrency is all about.
I will not vaguely compare it to mining. I will directly describe what happens inside the computer when we send, accept, and create cryptocurrencies.
I would also like to emphasize one point: although we will spend some time to understand the principles behind it, but if we only use it everyday, we don't need to understand the detailed technical principles, just like you don't need to know what happens behind your credit card. Everything is the same. Like electronic payments, cryptocurrencies also have many easy-to-use apps that can be used directly to send and receive currency without knowing how it is implemented.
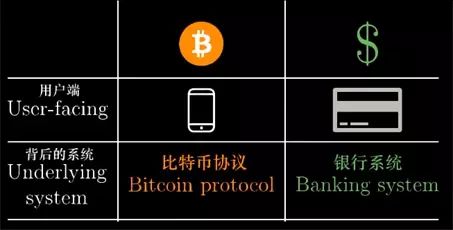
The difference is that behind the cryptocurrency is not a bank to verify the transaction, but a set of mathematical methods based on cryptography to verify the reliability of the transaction under decentralized, untrustworthy transactions.
Before you start speaking, you temporarily put the cryptocurrency aside. Let's start with a more basic concept: the book and the electronic signature.

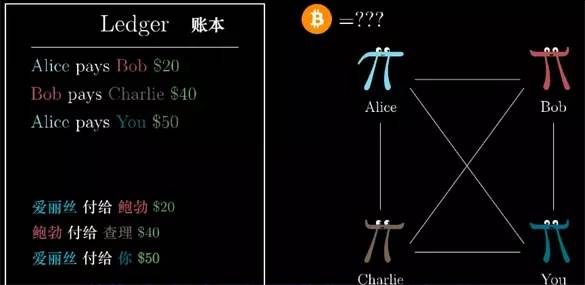
If you have frequent money with your friends, such as AA paying for dinner bills, etc., always using cash is always inconvenient. So you may use a public ledger: it records all that will be repaid in the future. The number, such as Alice pays Bob 20 yuan, Bob pays Charlie 40 yuan and so on.
This book must be open and accessible to everyone. Just like a website, everyone can access and add new transaction records. At the end of each month, everyone has no objection to the transaction record. If you can't make ends meet, you have to pay for it. If you still have a balance, you can get back the money you paid.
So the design of this simple system will probably be as follows: Everyone can add new transaction information to the ledger, and then settle it with real money at the end of the month.
But there is a problem with such a public ledger. Just because everyone can add transaction records, how should Bob be secretly recorded without Alice's consent: Alice gives Bob 100 yuan. (At the end of the month, Alice will Paying for the fabricated transaction)).
Why do we believe that the records in the books are accurate? Here, we need the electronic signature technology in cryptography. Just like handwritten signatures, Alice needs to be able to leave a record on the side of each transaction to prove that she understands and Recognize the occurrence of this transaction, and this signature cannot be obtained and forged by others.
Electronic signature ensures the authenticity of the transaction
It seems unlikely that electronic signatures will be realized. No matter how the electronic signatures are stored, the computer can read and copy them. How do you prevent counterfeiting? To achieve electronic signatures, everyone needs to generate a pair of keys: Public key and private key.
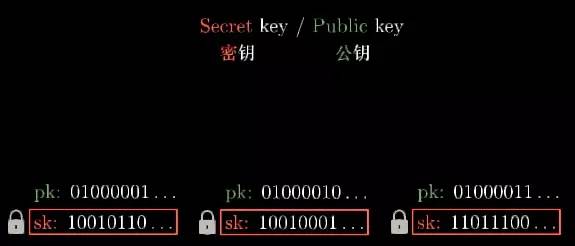
Each key is actually a string of 0 or 1 bit strings. The private key is sometimes called the "secret" key, so that it can be abbreviated to sk, and the public key is abbreviated to pk.
As the name suggests, the private key is kept by you. In real life, the signatures in all the documents you sign are the same. The electronic signature goes one step further, and it changes as the content of the signature changes. It looks like a bunch of 10 codes, usually 256 bits long. Any change in the character of the content to be encrypted will make the new signature generated by the string completely different.

Formally speaking, generating such a signature requires a function Sign, which requires both the signed content and your private key, that is, the Sign (signed content, key) → generates a new signature.
The private key ensures that only you can generate this electronic signature. The resulting signature also depends on what you want to sign, meaning that others cannot simply copy the signature and falsify another signature on other fabricated content ( Because the fabricated content is definitely different from the original content).

At the same time, there is a function Verify to verify whether the signature is true. This function requires three things: signed content, generated signature, public key. Its function is to tell us whether the signature is input. The key is generated corresponding to the private key.
This article does not specifically discuss how these functions are implemented ([Meeting Math] will be introduced in the future "Graphics Cryptography"), but it guarantees that if you don't know the private key of the other party, it is almost impossible to find a correct one. Signature. Accurately, it is only possible to find the correct signature by exhaustive and iterative verification, and then pass the verification with the public key pk.
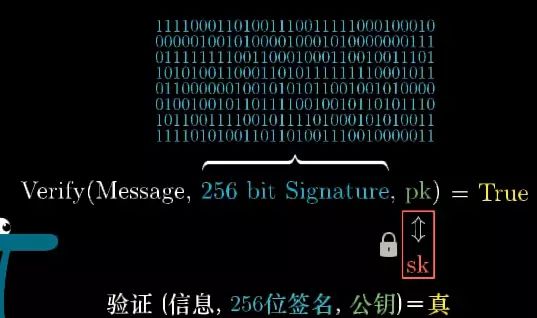
Now think about how many possible signatures are available for 256-bit bits. There are a total of 2256 possible signatures. This is an astronomical number. Calling it astronomical numbers actually overestimates the scope of astronomy. I also did Another supplemental video to demonstrate how big this number is, will be detailed later.
Now if you verify that a signature is true, you can quite confidently believe that the signature can only be generated by the private key that he holds.
Numbering ensures transaction uniqueness
Now it's ensured that everyone will sign the transaction information, but there will still be another problem, such as Alice signing a transaction that Alice pays Bob for $100, even if Bob can't forge a signature on Alice's new transaction record, he can Copy this record as many times as you like, because these records and their corresponding signatures are correct.
To solve this problem, when you sign each new transaction information, the transaction information must also contain a unique number corresponding to it. Then if Alice pays Bob 100 yuan multiple times, each record on the ledger will require one. New signature.

With electronic signatures, most of the trust crisis in the original system is solved, but to achieve it, you still need to rely on a similar credit institution, which means that you trust everyone to appear at the end of the month and settle in cash, because in case Charlie I owe a lot of money but I don’t have to pay back the money. This is the only reason people use cash to settle again at the end of the month - worrying that some people (like Charlie) owe a lot of money.
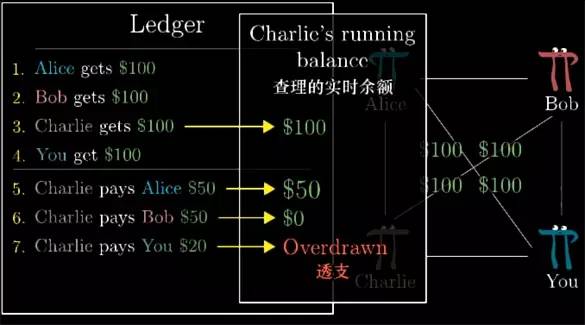
Smart, you think of a method, you don't need to actually use cash to settle, as long as you can avoid some of them spending less than the remaining payable amount. For example, everyone needs to pay 100 yuan to the account at the beginning, the first record on the ledger A few: Alice gets 100 yuan, Bob gets 100 yuan, Charlie and so on.

Now you only need to refuse to record on the books the transactions that some people can't make ends meet. For example, if the first two transactions are: Charlie pays Alice 50 yuan, Charlie pays Bob 50 yuan. Then if Charlie pays you 20 In the case of Yuan, the transaction will be invalid, which is invalid as if he had no signature.
However, this means that to verify the current transaction, you need to know all the historical transaction information as of now. This is also true in the cryptocurrency, and there is still room for optimization.
But what's interesting is that this design really removes the connection between the books and the real dollar. In theory, if everyone in the world uses this book, you can spend the whole life on the book and get the income, basically There is no need to get real money.
To emphasize this point, we refer to the currency unit on the ledger as the "book capital" and simply LD. Of course, you can also freely convert LD into real dollars at any time.
For example, Alice gave Bob $100 in reality, and Bob wrote Bob on the public ledger to pay Alice 100. But such redemption is not within the original design of the system, so it will not be protected by the agreement. Such exchanges are similar to the dollar and the euro or other currency exchanges in the market, that is another matter.
The core of Bitcoin
This is the most important information to understand Bitcoin and other cryptocurrencies. It is actually a book, and all historical transactions are treated as entities of money.
Of course, in terms of Bitcoin, people only use Bitcoin to buy and use Bitcoin to record on the ledger. But how does the new Bitcoin produce me?
But before that, our LD system has a different aspect from the actual cryptocurrency. I just mentioned that this public account book exists in a public place. For example, a website, everyone can log in and add records, then we have to Trust this central organization. Who is going to manage this website, and who controls the rules for adding records?
Considering that if you have access to this account, you don't need to trust the center. When you need to make a transaction, such as Alice paying Bob $100, you need to broadcast this information to all other people on the network. When I got this information, I wrote down the transaction on my own account.
This idea is simple, but it really is a bad design, because how to ensure that everyone has the right account.
When Bob received a deal like Alice paid Bob 10 LD, how did he ensure and believe that everyone else also received this information so that he could pay Charlie for the transaction with the 10 LD in the future?
Try to think about listening to the news broadcast from outside, how to ensure that others accept the transaction information in the same order as you, which is the key and an interesting problem.
You can come up with an agreement to decide whether to accept or reject the transaction information you receive, and you are sure that everyone else can accept the transaction information in the same order under this method, and eventually form the same bill, which is also the original paper in Bitcoin. Part of the details.
Simply put, Bitcoin gives the solution: Select the account that trusts the most computational resources (the most computationally). I will spend some time detailing what it means, it involves the concept of "cryptographic hash function" .

The basic idea is as follows: If you use the consumption of computing resources as the basis of your trust, then the cost of computing power in the case of inconsistent transaction records and books is too high to be feasible.
This idea is really cool! If you understand, you will understand the core of Bitcoin and other cryptocurrencies.
So first, what is a hash (hash) function? The input to these functions can be any information or file, they will output a fixed-length bit string, such as 256 bits, this output value is called the hash value of this information, or it is called "summary", it is deliberately designed to Outputs seemingly random, but not random, as long as the same information is always output the same content.
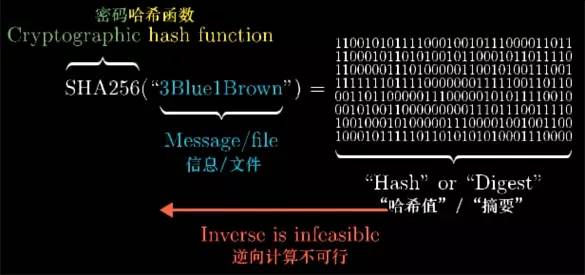
But if you change the input a little, maybe just modify one of the characters, the final hash value will become unrecognizable. In fact, the hash function I am demonstrating here is called "SHA256".
The slight modification of the input, the output will be completely different, there is no rule at all, understand, this is not a normal hash function, this is a cryptographic hash function, which means that reverse calculation is impossible.
If you are told a string of 256-bit 1,0 strings and then ask you, find the contents of the SHA256 function input, so that the two have the same result after passing through SHA256. You only have one method of violent trial and error.
But you want to feel how long it takes to calculate 2^256 times. You can check out this supplementary video (How safe is 256-bit encryption?) After a few days [Meet Math] will be sorted out).
You will think if you know the details of the operation of this function, you can not guess, but you can push back to guess this input. But no one can do it now.
Interestingly, there is no rigorous proof that reverse computing is difficult, but the current security industry and encryption requirements depend on the cryptographic hash function and its nature.
If you look closely at the encryption algorithm behind the encrypted connection established by the browser and youtube, or when the browser connects to the bank website, you will most likely see the SHA256 algorithm.
But now, our focus will be on how the spallation function proves that a series of transactions on the bill is related to a large amount of calculation.
Think if someone gives you a transaction record and says "Hey! I found a special number (the green number 1073765433 in the book below), you put this number behind the transaction record, and then give the whole After the transaction record information is calculated by the SHA256 function, the first 30 numbers will be 0!"

How hard is it to think about finding such a number? For a random piece of information, the probability that the first 30 bits of the hash value are 0 is one of the 30th power of 2, which is almost one billionth, and because SHA256 is a cryptographic hash function, find this The only way to do a special number is to be violent and exhaustive, so you have basically tried a billion times before you find this special number.
Once you know this number, quickly calculate the transaction list and the number together as input. After the hash calculation, it is found that the beginning is really 30 zeros.
In other words, you can quickly verify that they have actually gone through a lot of calculations, and you don't need to consume such a large amount of calculations yourself. This is called "work proof".
The important thing is that this workload proof itself corresponds to this transaction record. If you change one of the transaction information, even if you modify the column number, it will completely change the final hash value. So you need to go through one billion A second attempt can find a new proof of the workload - that is, find that special number, followed by your modified transaction list, so that the corresponding hash value starts with 30 zeros.

Now look back at the situation of our distributed ledger: everyone is broadcasting trading information, we want to find a way for everyone to recognize a correct bill. I said earlier that the core point of Bitcoin's original paper is Everyone trusts the bill that consumes the most amount of calculation.
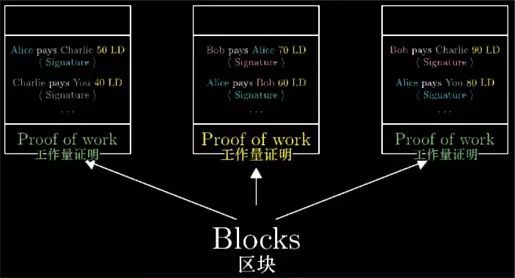
To implement this idea, you first need to organize the bills into "blocks." These blocks contain a series of transaction information and proof of its workload, that is, there is a special number that satisfies its hash value starting with a series of zeros.

Let's start with 60 zeros for the time being. We will look back later to see how to systematically determine the number of these zeros.
Analogous to the transaction information to be validated by the sender's signature, the same, a block is only considered valid when it has a proof of workload.
And to ensure that these blocks have a standard order, we specify that the hash value of the previous block must be added to the header information of the current block.
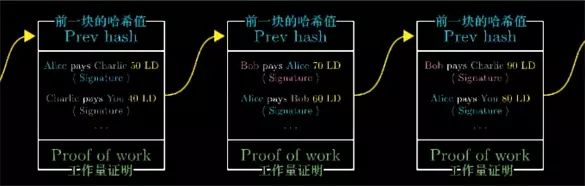
In this case, if you go back and want to change the contents of one of the blocks, or swap the order of the two blocks, you will change the content of the next block, and change the hash value of that block, then Also affects the next block...
This requires recalculating the hash values ​​of all of these blocks, re-finding each special number so that the hash value of the block starts with 60 zeros. Since all the blocks are linked to each other in this way, we generally do not It is called a ledger, but a "blockchain".
Under this new system, we now allow everyone in the world to participate in the construction of blocks, which means that they can listen to the transaction information in the network, organize the information to generate blocks, and then spend a lot of calculation work, find That special number makes the hash value of the block start with 60 zeros.
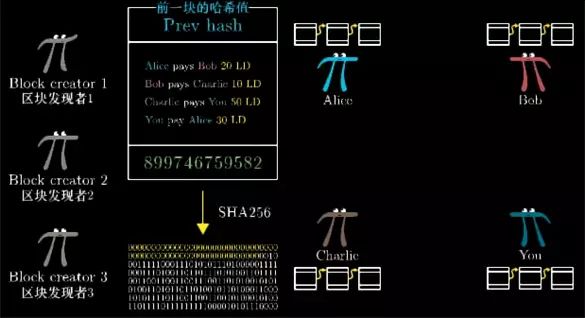
Once this number is found, they broadcast the block. To reward the block builder for the huge amount of computational effort, when she created a block, we specified that she could put a special transaction message At the beginning of the bill, that is, let her get 10 LD out of thin air. This is called "block reward", which does not belong to any transaction, it does not come from other people, so it does not need to be signed.
This also means that every new block will add new virtual currency. The building block is usually called “mining†because it will consume a lot of computing workload, and mining will introduce new currency for the entire economy. the amount.
So when you hear or see the miners, you now understand what they are doing: listening to trading information, building blocks, broadcasting blocks, and getting rewards for new currencies, that's all.
In the eyes of the miners, each block is like a small lottery ticket. Everyone wants to guess the special number as quickly as possible, until one of the lucky ones finds the special number, which allows the block to be scattered. Column values ​​start with a lot of 0s and they get rewards.
For those who just want to use this system to make transactions, you don't need to listen to the transaction records. They only need to listen to the blocks broadcast by the miners, and then update the blockchain they keep.
Now the key point of our agreement is coming. If we receive two completely different blockchains, in which the transaction information conflicts, you only keep the longest one, which is the one that contains the largest amount of work. (For example, if the blockchain length is 4 and 5, the length is 5).
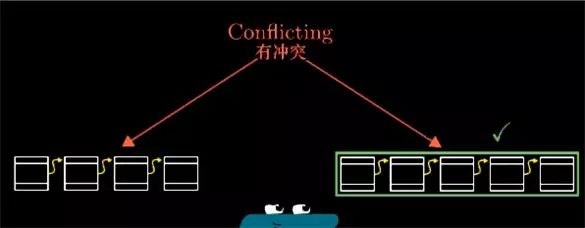
If it is difficult to divide up and down, waiting for the next block to broadcast, there will always be a longer blockchain, so even without a central authority, everyone will record their own blockchain, but if Everyone trusts the blockchain with the most workload, and we have reached a consensus on decentralization.
In order to understand why this system is credible, and how to believe that every transaction is true. We can actually understand, what to do in order to deceive under this system.
Maybe Alice wants to spoof Bob with a fake block, that is, she gives Bob a piece of information about her paying Bob 100 account in a block, but she didn't broadcast the block to other people on the network. Others thought she still held the 100 accounts. In order to do this, she would find a proof of work before all other miners could deceive everyone, because all the miners were also building blocks independently.
And this is indeed possible! It is possible that Alice has found this special number of calculations just before everyone else, but Bob will also receive block broadcasts from other miners. So in order to convince him of her forged block, Alice is behind It is necessary to continue to recalculate, all the blocks behind her block that were forged to Bob. These blocks and Bob received different blocks from other miners.
But the system agreement stipulates that Bob always trusts the longest blockchain he is referring to. Alice may still be ahead of the first few blocks - just happened to find that block before all other miners.
But unless she has nearly 50% of the computing resources of all miners, it is basically certain that the blocks calculated by all other miners will be longer than the blockchain formed by Alice forging Bob's blocks. fast.
So after a long enough time, Bob will reject the blockchain he received from Alice and choose the longest blockchain that everyone else is using.
Note that this means that you don't have to trust the new block you just received, but you should wait until there are new blocks added. If you haven't listened to the longer blockchain, you can trust This block does belong to the chain that everyone else is using.
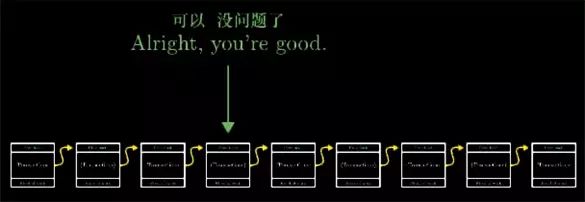
At this point, we explained all the main content, this distributed account book system based on workload proof, basically the working principle of Bitcoin and other cryptocurrencies. Let me talk more about the details, just let me talk about the workload proof. , is to find that special number, the hash value that satisfies its block starts with 60 0. In the actual bitcoin protocol, the theorem changes the number of 0, so that a new block can be generated every 10 minutes on average. .
As more and more miners join the ranks of "mining", the computational challenge is getting higher and higher. So that this small lottery ticket, only about every 10 minutes can be won by a person. Many new cryptocurrencies There is a shorter block time interval.

All Bitcoin in the Bitcoin system comes from the reward of generating new blocks. In the beginning, it is 50 bitcoins per block. There is also a website called "Block Explorer" that you can go and see. Seeing the information in the Bitcoin blockchain, if you look at the blocks that the blockchain first identified, they have no other deals besides the 50 bitcoins that are awarded to the miners.

But every 210,000 blocks, almost every 4 years, the block reward will be halved. Now, the reward for each block is 12.5 bitcoin, and because this reward decreases with time, it means The bitcoin that can be finally obtained will not exceed 21 million. But this is not to say that the miners will not make any money at the end. In addition to the block rewards, the miners can also get the transaction fee. Whenever you pay, you can choose a small transaction fee. Paying together, this transaction fee will eventually be given to the block builder who contains the record. You can encourage the miners to continue working and broadcast the block containing your transaction information to others on the network.
In Bitcoin, each block contains about 2,400 transaction records. Many critics think this limit is too strict. Compared with VISA, VISA processes about 1,700 transactions per second, and has the ability to process up to 24,000 per second. Trading. In contrast, Bitcoin's slower trading speed makes it more expensive to trade, and it is the transaction cost that determines which traders join the new block.
In addition to the basics of these cryptocurrencies, there are many other different cryptocurrency system designs that have not yet been covered, but I hope this video can be called the cornerstone of a solid curiosity. If you are interested, you can expand your reading and continue learning. As I At the beginning, the original intention of this video was because many funds poured into the cryptocurrency. I don’t think too much about good or bad, but I think people who want to enter this field know at least the basics of this technology. It should be very helpful.
How secure is 256 encryption?
In order to break a security system, you have to guess a 256-bit bit string. The first is in the electronic signature part, the second is mentioned in the cryptographic hash function.

For example, if you want to find a message that has a SHA256 hash value (hash value) equal to a 256-bit string, there is no other way to guerrilla and test the result. This requires an attempt
22,562,256 times.
This number is much larger than the number we usually encounter, so it's hard to understand its size. But let's try it, 22562256 is 232232, multiply it by 8 times.

The advantage of this decomposition is that we know that 232232 is about 4 billion.
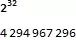
We can at least imagine the "small" number, um, come back to experience the concept of 4 billion consecutive multiplications of 8 times? Many people know that the GPU in our computer can perform a lot of parallel computing at a rapid speed. Therefore, please let the GPU repeatedly calculate the password hash function. A good performance GPU may calculate nearly 1 billion hashes per second. value.

If you take a bunch of such GPUs and let your supercomputer count 4 billion hashes per second, then the 4 billion that starts represents the number of hashes that your supercomputer calculates per second. .
Imagine 4 billion such supercomputers loaded with GPUs. Compared with Google, although Google has not announced the number of their servers, there are estimates that there are millions of them. In reality, most of their servers are not as good as ours. The computer with full GPU is strong. We assume that Google has replaced millions of servers with such supercomputers. Then 4 billion supercomputers are probably 1000 of these kind of Google after the blood. We call this computing power "Thousands of Google".

Looking further to the right, there are about 7.3 billion people in the world. Next we assume that more than half of the people (4 billion) have their own thousand Google.

Then imagine that 4 billion such planets, in contrast, the Milky Way has about 1,000 to 400 billion stars. Although we are not sure, the estimates are roughly in this range. So this is equivalent to 1% of the Milky Way stars, and each Half of the population on the planet has its own thousand Google.

Then imagine that 4 billion such a galaxy, we call it "100 million galaxy supercomputer", can guess 21,602,160 times per second.

4 billion seconds, about 126.8 years, it's 4 billion times, or 507 billion years, almost 37 times the age of the universe. So even if you have (GPU full of supercomputers) * (more than the average person on the planet has thousands of songs * (Planetary Aggregation) * (Billionaire Galaxy Computer) * (guessing 37 times the age of the universe), and only one billionth of a chance to guess the correct number.
Principle of cryptography

Those who know what public key cryptography may have heard of ECC, ECDH or ECDSA. The first term is an abbreviation for Elliptic Curve Cryptography, and the last two are based on its algorithm name.
Today, we can see elliptic curve cryptography in TLS, PGP, and SSH, which are the three main technologies that the modern network and IT world rely on. Bitcoin and other cryptocurrencies are encrypted using this encryption algorithm.
Before the ECC became popular, almost all public key algorithms were based on RSA, DSA, and DH -- an optional encryption system based on modulo operations. RSA and its friend algorithms are still very important at the moment and are often used in conjunction with ECC. However, the principles behind RSA and its friend algorithms are easy to explain, so they are widely understood, and some simple implementations can be easily written; but the implementation of ECC is still mysterious to most people.
Through a series of blog posts, I intend to introduce elliptic curve cryptography in a popular way. My goal is not to provide complete and detailed guidance for ECC (sufficient information on the web), but a brief overview of "what is ECC and why it is considered safe", avoiding wasting time on lengthy mathematical proofs and annoying The implementation details. I will also provide some helper examples as well as visual graphical tools and scripts for everyone to use.
Specifically, I will touch on the following topics:
1. Elliptic curves and group axioms based on real numbers (involved in this article)
2. Elliptic curve and discrete logarithm problem based on finite field
3. Key pair generation and two ECC algorithms: ECDH and ECDSA
4. Algorithms that destroy ECC security and compare it with RSA
In order to understand the content described in this article, you need to understand the basic concepts of set theory, geometry, modulo operations, and roughly understand symmetric and asymmetric encryption. In addition, you need to know clearly what is "easy to solve", what is "difficult" and their role in cryptography.
Ready? Start!
Elliptic curve
First of all, what is an elliptic curve? The MathWorld online math encyclopedia gives an excellent and complete definition. However, for our learning purposes, the elliptic curve will be reduced to a collection of points described by this equation:
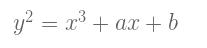
Among them, 4a3 + 27b2 ≠0 (this is to exclude odd curves). The above equation is called the Weierstrass normal form of the elliptic curve.

Different shapes of different elliptic curves (b = 1, a varies from 2 to -3).
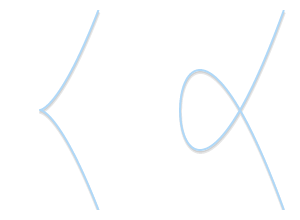
Singularity type: Left side, curve with a sharp corner (y2 = x3). On the right side, with a self-intersecting curve (y2 = x3 – 3x + 2). Neither of these is a valid elliptic curve.
According to the values ​​of a and b, the elliptic curve can assume different shapes on the plane. It can be easily seen and verified: The elliptic curve is symmetric about the x-axis. To achieve our goal, we also need to treat an infinity point (also called the ideal point) as part of an elliptic curve. From now on, we will use the symbol 0 (zero) to represent the infinity point.
If we want to explicitly consider the infinity point, we can refine the definition of the elliptic curve as follows:
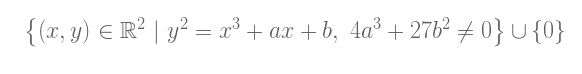
group
The "group" in mathematics is a set of binary operations defined by us. The binary operation is called "addition" and is represented by the symbol "+". In order for a set G to be a group, you must define an addition and have the following four characteristics:
1. Closedness: If a and b are elements in set G, then (a + b) is also an element in set G.
2. Combination law: (a + b) + c = a + (b + c);
3. There is a unit 0, so that a + 0 = 0 + a = a;
4. Each element has an inverse element, ie for any a, there is b such that a + b = 0.
If we add the fifth condition:
5. Exchange law: a + b = b + a
Then, call this group an abelian group.
When combined with the usual concept of addition, the set Z of integers is a group (also an Abelian group). The set of natural numbers (N) is not a group because it does not satisfy the fourth characteristic.
"Group" is useful because once we prove that it has the above four characteristics, then we are free to get some other features. For example, the unit cell is unique; in addition, the inverse element is unique, that is, for each a, there is a unique b, so that a + b = 0 (we can write b as -a). Later we will find that these characteristics of the group and other existing facts, either directly or indirectly, are very important to us.
Group axiom of elliptic curve
We can define a group based on an elliptic curve. as follows:
• The element in the group is a point on an elliptic curve;
• The unit cell is infinity point O;
• The inverse of point P is its symmetry point about the x-axis;
• Addition, which satisfies the following rules: For 3 non-zero points P, Q and R on the same line, their sum P + Q + R = 0.

The sum of the three points on the same line is equal to 0.
Looking at the last rule, all we need is three points in the same line, regardless of the order of the points. This means that if P, Q and R are in line, then P + (Q + R) = Q + (P + R) = R + (P + Q) = • • • = 0. In this way, we visually prove Our "+" operation satisfies both the conjunction and the exchange law: we created an Abelian group.
It is still very good so far. But how do we actually calculate the sum of any two points?
Geometric addition
Thanks to the fact that we are using an Abelian group, we can write P + Q + R = 0 as P + Q = –R. This form of the equation allows us to derive a geometric method for calculating the sum of two points P and Q: draw a line passing through the P and Q points, which intersects the curve to get the third point R (this fact means P, Q, R must be collinear). If we get the inverse -R of this point, then we get the result of P + Q.
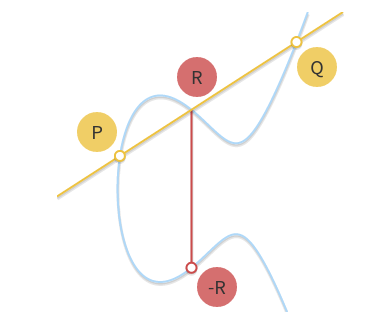
Draw a straight line through P and Q. The line intersects the curve with the third point R. The point symmetry -R is the result of P+Q
This geometric approach can be established, but some improvements are needed. In particular, we need to answer the following questions:
• What to do when P = 0 or Q = 0? Obviously, we cannot draw any straight line (0 is not on the xy-plane). However, since we define 0 points as the unit cell, for any P and any Q, there are: P + 0 = P , 0 + Q = Q
• What to do when P= –Q? In this case, the line passing through the two points is a vertical line and there is no third intersection with the curve. However, since P is the inverse of Q, then P + Q = P + (-P) = 0 can be known from the definition of inverse.
• What to do when P = Q? In this case, there are countless straight lines passing through that point. Things started a bit complicated. However, Imagine a point Q' ≠P first. What if we make Q' approach P, getting closer and closer to P?
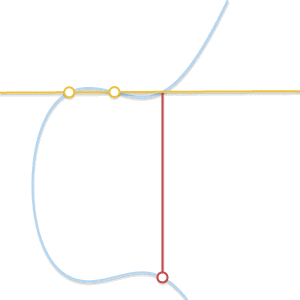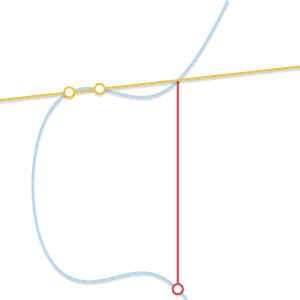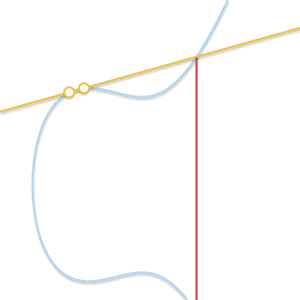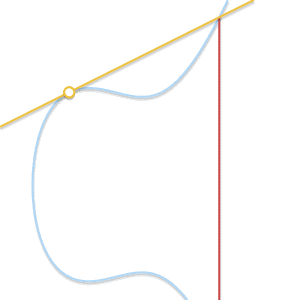
As the two points get closer and closer, the line passing through these two points eventually becomes the tangent of the curve.
As Q' tends to P, the line passing P and Q' eventually becomes the tangent to the curve.看到这一点,我们å¯ä»¥å®šä¹‰P + P = –R, å…¶ä¸R是过P点的切线与曲线的交点。
• 当P ≠Q,但找ä¸åˆ°ç¬¬ä¸‰ä¸ªç‚¹R时怎么办? è¿™ç§æƒ…况和上é¢é‚£ä¸ªéžå¸¸ç±»ä¼¼ã€‚å®žé™…ä¸Šï¼Œè¿™æ˜¯å› ä¸ºè¿‡På’ŒQ的直线与曲线相切。
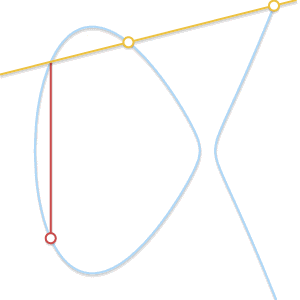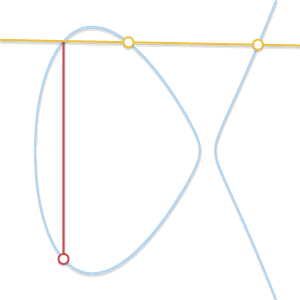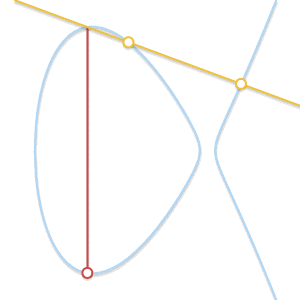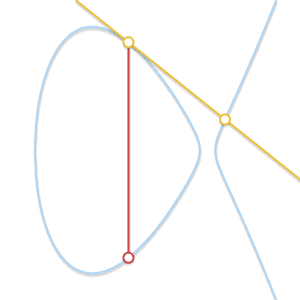
如果直线与曲线åªæœ‰ä¸¤ä¸ªäº¤ç‚¹ï¼Œé‚£ä¹ˆè¯¥ç›´çº¿ä¸ºæ›²çº¿çš„切线。å¯ä»¥å¾ˆå®¹æ˜“åœ°çœ‹å‡ºï¼Œä¸¤ç‚¹ç›¸åŠ çš„ç»“æžœæ˜¯å…¶ä¸ä¸€ç‚¹çš„对称点
• å‡è®¾P是切点,在上一情况ä¸ï¼Œæˆ‘们已ç»å¾—出P + P = –Q. ç‰å¼çŽ°åœ¨å˜ä¸ºP + Q = –P。 如果Q 是切点,æ£ç¡®çš„ç‰å¼åº”为P + Q = –Q.
çŽ°åœ¨ï¼Œç”¨å‡ ä½•æ–¹æ³•å¯ä»¥å®Œå…¨è¦†ç›–所有情况了。用一支铅笔和一把尺,我们å¯ä»¥åšä»»æ„æ¤åœ†æ›²çº¿ä¸Šæ‰€æœ‰ç‚¹çš„åŠ æ³•è¿ç®—ã€‚å¦‚æžœä½ æƒ³è¯•è¯•ï¼Œè¯·åˆ°HTML5/JavaScript visual tool 看一下,这是我建的一个工具,用æ¥è®¡ç®—æ¤åœ†æ›²çº¿çš„åŠ æ³•!
ä»£æ•°åŠ æ³•
å¦‚æžœæˆ‘ä»¬æƒ³æŠŠç‚¹çš„åŠ æ³•è¿ç®—计算机æ¥å®Œæˆï¼Œé‚£ä¹ˆéœ€è¦å°†å‡ 何方法转化为代数方法。将上é¢æ述的规则转æ¢ä¸ºä¸€ç»„å…¬å¼çœ‹ä¼¼ç®€å•ï¼Œå®žé™…上是éžå¸¸ç¹ççš„ï¼Œå› ä¸ºéœ€è¦æ±‚è§£ä¸‰æ¬¡æ–¹ç¨‹ã€‚å› æ¤ï¼Œè¿™é‡Œæˆ‘åªé€šæŠ¥ç»“果。
首先,先抛开最æ¼äººçš„æžç«¯æƒ…况。我们已ç»çŸ¥é“P + (-P) = 0, 还知é“P + 0 = 0 + P = P。所以,在我们的公å¼ä¸ï¼Œæˆ‘们将é¿å…这两ç§æƒ…况,åªè€ƒè™‘两个éžé›¶ã€éžå¯¹ç§°ç‚¹P = (xP, yP) å’ŒQ = (xQ, yQ).
如果P å’ŒQ ä¸ç›¸åŒï¼Œ (xP ≠xQ), 过这两点的直线斜率为:
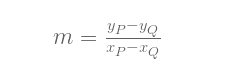
该直线与æ¤åœ†æ›²çº¿äº¤äºŽç¬¬ä¸‰ç‚¹R = (xR, yR):
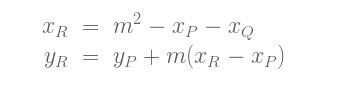
或是, ç‰ä»·å½¢å¼:
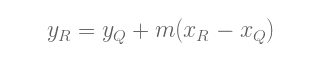
å› æ¤ï¼Œ(xP, yP) + (xQ, yQ) = (xR, –yR) (注æ„æ£è´Ÿå·ï¼Œè®°ä½P + Q = –R).
如果我们想检查这一结果是å¦æ£ç¡®ï¼Œæˆ‘们将ä¸å¾—ä¸æ£€æŸ¥R是å¦åœ¨æ›²çº¿ä¸Šï¼ŒåŒæ—¶Pã€Qã€Q是共线。检查点是å¦å…±çº¿è½»è€Œæ˜“举,但检查R是å¦åœ¨æ›²çº¿ä¸Šå°±ä¸å®¹æ˜“äº†ï¼Œå› ä¸ºéœ€è¦æ±‚解三次方程,这å¯ä¸æ˜¯ä»€ä¹ˆå¥½çŽ©çš„事儿。
ä¸è¿‡ï¼Œæˆ‘们å¯ä»¥ç”¨ä¸€ä¸ªä¾‹åæ¥è¯•ä¸€ä¸‹ï¼šæ ¹æ®å¯è§†åŒ–工具的计算, 当P = (1, 2) ã€Q = (3, 4) ,æ¤åœ†æ›²çº¿y2 = x3 – 7x + 10, 两点之和P + Q = –R = (-3, 2). 让我们看一下与我们的公å¼æ˜¯å¦ä¸€è‡´:
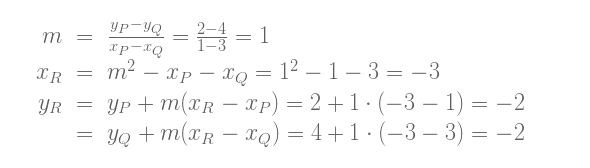
好的,æ£ç¡®!
注æ„上é¢çš„å…¬å¼å³ä½¿åœ¨å…¶ä¸ä¸€ä¸ªç‚¹P或Q是切点的情况下也æˆç«‹ã€‚让我们试一下P = (-1, 4) 〠Q = (1, 2).
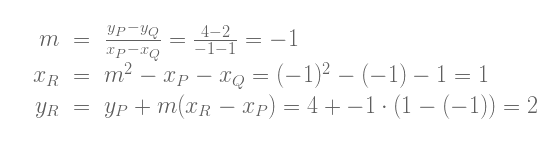
我们计算出P + Q = (1, -2), 与使用å¯è§†åŒ–工具计算出的结果相åŒã€‚
P = Q 的情况需è¦åšç‚¹ä¸åŒçš„处ç†ï¼šæ–¹ç¨‹ä¸xR å’ŒyR 相åŒ, 由于xP = xQ, 我们必须使用ä¸åŒçš„å…¬å¼æ¥è®¡ç®—斜率:
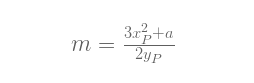
注æ„,我们å¯ä»¥æ–™åˆ°ï¼Œm的表达å¼å®žé™…是下é¢è¿™ä¸ªå‡½æ•°çš„一阶导数:
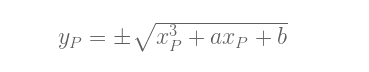
为了è¯æ˜Žç»“果的有效性,åªè¦æ£€æŸ¥R是å¦åœ¨æ›²çº¿ä¸Šï¼Œä»¥åŠPå’ŒR在曲线上åªæœ‰ä¸¤ä¸ªäº¤ç‚¹å°±è¶³å¤Ÿäº†ã€‚但åŒæ ·ï¼Œæˆ‘们ä¸åŽ»è¯æ˜Žè¿™ä¸€äº‹å®žï¼Œè€Œæ˜¯è¯•ç®—一个例å: P = Q = (1, 2).
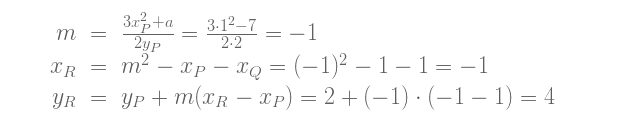
å…¬å¼è®¡ç®—出P + P = –R = (-1, -4).æ£ç¡®!
尽管推导过程真的是æžå…¶ç¹ç,ä¸è¿‡æœ€åŽçš„å…¬å¼è¿˜æ˜¯å¾ˆç®€æ´ã€‚è¿™è¦æ„Ÿè°¢é尔斯特拉斯范å¼ï¼šè¦æ˜¯æ²¡æœ‰è¿™ä¸€èŒƒå¼ï¼Œæœ€åŽçš„å…¬å¼ä¼šçœŸçš„åˆé•¿åˆå¤æ‚。
æ ‡é‡ä¹˜æ³•
åœ¨åŠ æ³•ä¹‹å¤–ï¼Œæˆ‘ä»¬è¿˜å¯ä»¥å®šä¹‰å¦ä¸€ç§è¿ç®—ï¼šæ ‡é‡ä¹˜æ³•ï¼Œå³ï¼š
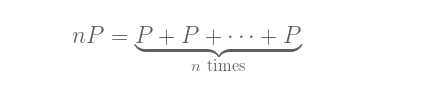
nP,其ä¸nä¸ºè‡ªç„¶æ•°ã€‚æˆ‘ä¸ºæ ‡é‡ä¹˜æ³•ä¹Ÿå†™äº†ä¸ªå¯è§†åŒ–å·¥å…·ï¼Œå¦‚æžœä½ æƒ³è¯•ç®—æ—¶å¯ä»¥ä½¿ç”¨ã€‚
用这ç§å½¢å¼è¡¨ç¤ºæ—¶ï¼Œè®¡ç®—nP似乎需è¦næ¬¡åŠ æ³•è¿ç®—。如果n有k个二进制ä½ï¼Œé‚£ä¹ˆç®—法的时间å¤æ‚度将为O(2^k),这真ä¸æ˜¯å¾ˆå¥½ã€‚ä¸è¿‡å˜åœ¨ä¸€äº›æ›´å¿«çš„算法。
å…¶ä¸ä¸€ç§æ˜¯â€œåŠ å€ï¼ˆdouble)ä¸Žç›¸åŠ ï¼ˆadd)â€ç®—法。
计算的原ç†å¯ä»¥ç”¨ä¸€ä¸ªä¾‹åæ¥æ›´å¥½åœ°è§£é‡Šã€‚å–n = 151。它的二进制表示形å¼ä¸º100101112 。这一二进制表示形å¼å¯ä»¥è½¬æ¢ä¸ºä¸€ç³»åˆ—2的幂之和。
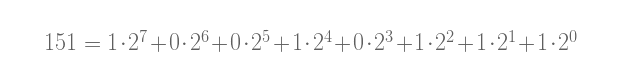
(å–nçš„æ¯ä¸ªäºŒè¿›åˆ¶ä½ä¸Šçš„æ•°å—,并用它乘以一个2的幂.)
用这ç§æ–¹æ³•ï¼Œæˆ‘们å¯ä»¥å°†nè¿™æ ·å†™:
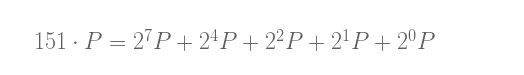
â€œåŠ å€ï¼ˆdouble)ä¸Žç›¸åŠ ï¼ˆadd)â€ç®—法需è¦è¿™æ ·åš:
• å–P.
• åŠ å€ï¼Œå¾—到2P.
• 2P与Pç›¸åŠ (为了得到21P + 20P).
• åŠ å€2P,得到22P.
• 与å‰ä¸€ç»“æžœç›¸åŠ (得到22P + 21P + 20P).
• åŠ å€22P,得到23P.
• 对23Pä¸åšä»»ä½•æ“作.
• åŠ å€23P,得到24P.
• 与å‰ä¸€ç»“æžœç›¸åŠ (得到24P + 22P + 21P + 20P).
• …
最åŽï¼Œæˆ‘们å¯ä»¥è®¡ç®—151 • P ,åªéœ€7æ¬¡â€œåŠ å€â€è¿ç®—å’Œ4æ¬¡â€œç›¸åŠ â€è¿ç®—。
如果还ä¸å¤Ÿæ¸…楚,这里有一个实现该算法的python代ç 段:

å¦‚æžœâ€œåŠ å€â€å’Œâ€œç›¸åŠ â€æ“作å¤æ‚度å‡ä¸ºO(1),那么该算法的时间å¤æ‚度为O(log n) (或是O(k),如果我们考虑的是二进制ä½çš„长度),这相当ä¸é”™ã€‚比最åˆO(n)的算法肯定è¦å¥½å¾—多。
对数
给定nå’ŒP, 我们现在至少有一个多项å¼æ—¶é—´ç®—法æ¥è®¡ç®—Q = nP。ä¸è¿‡ï¼Œé€†è¿ç®—需è¦è®¡ç®—多少轮呢?如果已知Qå’ŒP,我们想求解nä¼šæ€Žä¹ˆæ ·ï¼Ÿè¿™ä¸€é—®é¢˜è¢«ç§°ä¸ºå¯¹æ•°é—®é¢˜ã€‚æˆ‘ä»¬ç§°ä¹‹ä¸ºâ€œå¯¹æ•°â€è€Œä¸æ˜¯â€œé™¤æ³•â€æ˜¯ä¸ºäº†ä¸Žå…¶ä»–åŠ å¯†ç³»ç»Ÿï¼ˆåœ¨æœ¯è¯ä¸Šï¼‰ä¿æŒç»Ÿä¸€ï¼ˆé‚£äº›ç³»ç»Ÿä¸ï¼Œä¸ç§°â€œä¹˜æ³•â€ï¼Œè€Œç§°â€œå¹‚â€ï¼‰ã€‚
我ä¸çŸ¥é“任何关于对数问题的“易解â€ç®—法,ä¸è¿‡ï¼Œé€šè¿‡æ‘†å¼„乘法,很容易å‘现一些模å¼ã€‚例如,对于曲线y2 = x3 – 3x + 1和点P = (0, 1). 我们å¯ä»¥ç«‹å³éªŒè¯å‡º, 如果n为奇数,nP在曲线的左åŠé¢ï¼Œå¦‚æžœn为å¶æ•°ï¼ŒnP在曲线的å³åŠé¢ã€‚如果我们å°è¯•æ›´å¤šæ¬¡ï¼Œæˆ‘们或许å¯ä»¥æ‰¾å‡ºæ›´å¤šçš„模å¼ï¼Œæœ€ç»ˆå¯ä»¥è®©æˆ‘们写出一个算法æ¥é«˜æ•ˆè®¡ç®—é‚£æ¡æ›²çº¿çš„对数问题。
ä¸è¿‡ï¼Œå¯¹æ•°é—®é¢˜æœ‰ä¸€ä¸ªå˜ä½“:离散对数问题。在下一篇åšæ–‡ä¸ï¼Œæˆ‘们将看到,当我们对æ¤åœ†æ›²çº¿çš„域进行缩å‡åŽï¼Œæ ‡é‡ä¹˜æ³•ä»æ—§â€æ˜“解“,而离散对数问题æˆä¸ºäº†â€éš¾è§£â€é—®é¢˜ã€‚è¿™ç§åŒé‡æ€§æ˜¯æ¤åœ†æ›²çº¿å¯†ç å¦çš„关键基石。
Bitmain Antminer Asic Miner:Bitmain Antminer Z15,Bitmain Antminer Z9 Mini,Bitmain Antminer Z9,Bitmain Antminer Z11
Bitmain is the world's leading digital currency mining machine manufacturer. Its brand ANTMINER has maintained a long-term technological and market dominance in the industry, with customers covering more than 100 countries and regions. The company has subsidiaries in China, the United States, Singapore, Malaysia, Kazakhstan and other places.
Bitmain has a unique computing power efficiency ratio technology to provide the global blockchain network with outstanding computing power infrastructure and solutions. Since its establishment in 2013, ANTMINER BTC mining machine single computing power has increased by three orders of magnitude, while computing power efficiency ratio has decreased by two orders of magnitude. Bitmain's vision is to make the digital world a better place for mankind.
Bitmain Antminer Asic Miner,Z15 bitmain antminer,Z11 Antminer Bitmain,zcash miner,zec mining machine
Shenzhen YLHM Technology Co., Ltd. , https://www.asicminer-ylhm.com