The basis pursuit algorithm is an algorithm used to solve the equality constraint problem where the unknown parameter L1 norm is minimized.
Basis tracking is a method of sparseening known coefficients commonly used in signal processing. The solution of transforming the L0 norm to L1 norm in the optimization problem is the basic idea of ​​basis tracking.
For example, I originally had an optimization problem:
min || x || _0 (the minimum value of the L0 norm) subject to y = Ax.
This || x || _0 means how many non-zero elements there are in x; then we require min || x || _0, which is to know what is the solution x that contains at most 0 elements.
However, the L0 norm is non-convex and not very easy to solve. At this time, we turn to the L1 norm optimization problem.
Then, the basic tracking algorithm is to solve instead
min || x || _1 (which is the minimum value of the L1 norm) subject to || y-Ax || _2 = 0 (2 norm)
This || x || _1 is the absolute value of x; then we require min || x || _1, which is to find the solution x with the smallest absolute value.
More generally, for example, I request a system of linear equations
Ax = b
x is the unknown quantity we require. This A matrix is ​​not a square matrix, but an under-determined matrix, so this linear equation system will have several sets of solutions. So which group should we solve?
If under normal circumstances, you can directly use least squares to obtain a set of least squares solutions, that is x = (A'A) ^ (-1) A'b. But now we use basis tracking, we want to get a set of solutions with the most 0 elements.
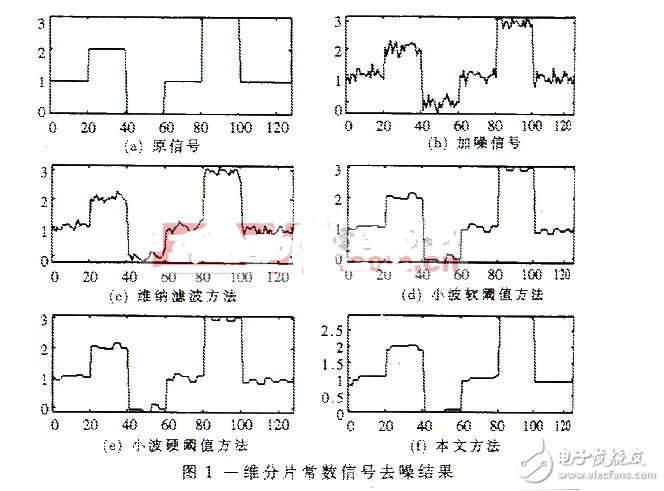
A new basis tracking algorithm is proposed. The dictionary is adaptively selected according to the signal characteristics; through the approximate representation of the l1 norm, the constrained extremum problem is transformed into an unconstrained problem, and a new iterative algorithm is used to quickly solve it; the experimental results of several typical signal types are verified This method has a good denoising effect. Keywords: base tracking dictionary denoising base tracking method is a new method in the field of sparse signal representation. It seeks to get the most sparse representation of the signal from the complete (over-complete) function (base) set, that is, to represent the original signal accurately with as few bases as possible, thereby obtaining the inherent nature of the signal. The basis tracking method uses the norm of the representation system as a measure of signal sparsity. The signal sparse representation problem is defined as a type of constrained extremum problem by minimizing the l1 norm, and then transformed into a linear programming problem for solution. At present, the basic tracking method has good application in the field of one-dimensional signal processing.
The working group of the Department of Statistics of the University of Ford Demand, represented by David L. Donoho, used the base tracking method to obtain many good application results in one-dimensional real signal denoising and super resolution. Despite the use of a new linear programming algorithm, the interior point algorithm, the base tracking method still requires a large amount of computation due to minimizing a global objective function in all dictionary vectors. Because of the difficulty in solving large-scale linear programming problems, current base tracking methods are limited to one-dimensional signal denoising and super-resolution processing. This paper proposes a new idea to solve the above-mentioned constrained extreme value problem. First, the dictionary is adaptively selected according to the signal characteristics; through the approximate representation of the l1 norm, the constrained extremum problem is transformed into an unconstrained problem, and an iterative algorithm is used to quickly solve it; finally, several typical signal denoising experiments To verify the application effect of this method. Experimental results show that the improved basis tracking method can be realized quickly and stably. At the same time, it has a good denoising effect.
For the observed discrete signal s ∈ H, H is Hilbert space, given the dictionary φ = {φγ, γ∈Γ} in H, where Γ is the index set, and φγ is the basis function in H, also called atom. The basis tracking method defines the signal sparse representation problem as the following extreme value problem with end, namely

Among them, α γ (γ ∈ Γ) represents the coefficient. If the vector in the dictionary is represented as an example of matrix φ and the coefficient is represented as a column vector, then (1) can be expressed as min || α || 1 subject to s = φα (2) In the case of noisy observations Consider the following model: y = s + σz where s is the real signal, y is the observed signal, z is the standard Gaussian white noise, and σ is the noise root variance. Basis tracking method denoising comes down to solving the following optimization problem:

The above optimization problem is dedicated to minimizing the signal reconstruction error, and at the same time making the signal representation sparse. The regularization parameter λ controls the balance between allowable error and sparsity. It can be seen from equation (3) that the core problem of denoising based on the base tracking method involves three aspects: the selection of atoms, the construction of the dictionary, and the design of the solution algorithm. Among them, the construction of the dictionary is an important part of the base tracking method. In order to represent the signal as accurately as possible, the dictionary and the signal application are adaptive, or the bytes are obtained from the signal learning. Generally, the dictionaries used by the base tracking method are complete, over-complete, and under-complete. The dictionary can be designed according to the a priori information of the signal and the actual needs. Generally designed dictionaries are complete or over-complete. For simple signal denoising, generally only a complete dictionary needs to be constructed. For the noise of composite signals, it is usually necessary to construct a complete dictionary. For the complete dictionary, there is also the problem of sparse representation of the signal, because the noise is always bizarre. The main dictionaries used in this article are: (1) Heaviside dictionary
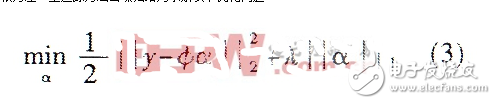
The atoms in this dictionary are not orthogonal, but for a one-dimensional discrete signal s = (s1s2 ... sn) of any length n:

The Heaviside dictionary has an upper triangular form, a simple structure, and is good at capturing the abrupt characteristics in the slice constant signal. (2) Time-scale dictionary (wavelet dictionary) Take Haar wavelet dictionary as an example: Your wavelet base: ψ = l [0,1], mother wavelet base: ψ = 1 [1 / 2,1], 1-1 [ 0, 1/2] Haar wavelet dictionary contains translation and expansion transformation of wavelet basis and translation transformation of wavelet basis. Let ψ = (a, b, v), where α ∈ (0, ∞) is a scale variable, b ∈ [0, n] represents position, and v ∈ {0, 1} represents gender. The Haar wavelet dictionary form is:
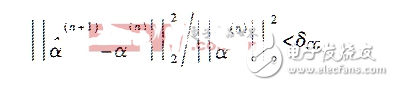
Contains n atoms, forming a set of orthogonal basis. Of course, there are other types of wavelet dictionaries. Although some wavelet bases do not have explicit wavelet function expressions like Haar wavelet bases, their dictionaries have discrete structures similar to Haar wavelet dictionaries. The more commonly used are Daubechies, Coiflet, Symmlet, etc. The wavelet dictionary is used to represent the piecewise smooth signal. (3) Heaviside dictionary + wavelet dictionary For more complex composite signals, the most sparse representation of the signal cannot be obtained under a single dictionary. At this time, several dictionaries can be synthesized to obtain an over-complete dictionary. For example Heaviside dictionary + wavelet dictionary.
Aluminum Alloy Support,Speaker Alloy Stands,Bookshelf Speaker Alloy Stands,Studio Monitor Alloy Stands
Dongguan Metalwork Technology Co., LTD. , https://www.diecast-pro.com