In the encoding of a set of numbers, if any two adjacent codes have only one binary number different, the code is called Gray Code, and there is only one bit between the maximum number and the minimum number. Different, that is, "end-to-end", so it is also called cyclic code or reflection code. In digital systems, code is often required to change in a certain order. For example, counting by natural number, if 8421 code is used, the number of bits will change when the number 0111 changes to 1000. In the actual circuit, the change of 4 bits cannot be absolutely simultaneous, and other codes may appear in the count. (1100, 1111, etc.). In certain cases, it may cause a circuit status error or an input error. This error can be avoided by using Gray code. Gray code is available in a variety of coding formats.
Gray Code used Grey Code, Gray code, Gree code, Golay code, cyclic code, reflection binary code, minimum error code and other names. Some of them are wrong, some are easily confused with other names. It is recommended not to use these used names.
BinaryBinary is a number system widely used in computing technology. Binary data is a number represented by two numbers 0 and 1. Its cardinality is 2, the carry rule is "every two into one", and the borrowing rule is "borrowing one and two", discovered by the 18th century German mathematical philosophy master Leibniz. Current computer systems use essentially binary systems, and data is stored primarily in the form of complements in the computer. The binary in the computer is a very small switch, with "on" to indicate 1, "off" to indicate 0.
The invention and application of computers in the 20th century, known as one of the important symbols of the third technological revolution, because digital computers can only be identified and processed by '0'. The code consisting of the '1' symbol string. Its operation mode is binary. In the 19th century, the Irish logician George Boolean thought of the process of thinking about logical propositions into some algebraic calculus for the symbol "0''. ''1'', binary is the carry system of the binary carry. 0, 1 is the basic operator Because it only uses 0, 1 two-digit symbols, it is very simple and convenient, and easy to implement electronically.
Decimal 586 = binary 1001001010 = Gray code 1101101111.
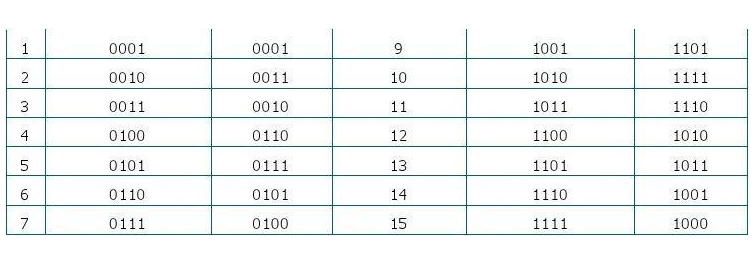
Binary code -----" Gray code (code):
From the rightmost bit, each bit is XORed with the left bit as the value corresponding to the Gray code, and the leftmost bit is unchanged (equivalent to 0 on the left).
The characteristics of Gray code are:
The adjacent two numbers of Gray code have only one bit change.
Moreover, there is only one binary change in the minimum and maximum values ​​within its range.
For example, the following two numbers:
Minimum: binary 0000 = Gray code 0000
Maximum: Binary 1111 = Gray code 1000
I saw it, 0000 and 1000, only one digit changed.
-------
If the decimal is first converted to BCD code during the conversion process, this loses the characteristics of Gray code.
Because in the BCD code:
Minimum: binary 0000 = Gray code 0000
Maximum: Binary 1001 = Gray code 1101
It can be seen that there are three changes between them.
The Gray code is changed by the BCD code, and the idea is wrong. The transformed is not the original Gray code.
Convert natural binary numbers to Gray code
------------
There is an N-bit binary number B(i), where 0 "= i "= N - 1; it can be transformed into the same number of Gray code G(i).
The conversion formula for binary numbers and Gray codes is as follows:
G(i) = B(i+1) XOR B(i) ; 0 <<= i << N - 1
G(i) = B(i) ; i = N - 1
If you are transforming through programmatic calculations, you need to use this formula to calculate bit by bit;
If you are using a hardware circuit to transform, you can use the circuit given earlier in answering the question.
Gray code conversion to natural binary number
------------
With the N-bit Gray code G(i), the algorithm for converting it to a natural binary number is as follows.
The highest bit of the natural binary code is equal to the highest bit of the lightning code;
The second highest bit of the natural binary code is the highest bit natural binary code and the next highest bit Gray code is different;
The rest of the natural binary code is similar to the second highest natural binary code.
The conversion formula is as follows:
B(i) = G(i) ; i = N - 1
B(i) = B(i+1) XOR G(i) ; 0 <<= i << N - 1
Mc4 Solar Connector,Mc4 Connect,Mc4 Branch Connector,Mc4 Y Connector
Sowell Electric CO., LTD. , https://www.sowellsolar.com