What is linear algebra?
In university mathematics, linear algebra is the most abstract subject. The thinking span from elementary mathematics to linear algebra is much larger than calculus and probability statistics. After learning, many people stay at the stage of knowing what is happening and not knowing why. After a few years, they found that the application of linear algebra is ubiquitous after contacting graphics programming or machine learning, but they still suffer from not being able to understand and master it well. Indeed, most people can easily understand the various concepts of elementary mathematics. Functions, equations, and sequence of numbers are all so natural, but when entering the world of linear algebra, it is like entering another strange world, in various strange symbols and operations. Lost in it.
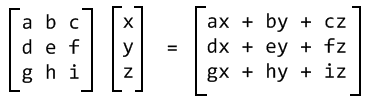
When I first came into contact with linear algebra, I almost felt that this was a subject that was flying away from the sky, and a question emerged in my mind:
Is linear algebra an objective natural law or a man-made design?
If you see this question, your reaction is "I still have to ask, mathematics is of course an objective law of nature", I don't think it is strange at all, I have thought so myself. From elementary mathematics and elementary physics in middle school, few people doubt whether a subject of mathematics is a natural law. When I studied calculus and probability and statistics, I never doubted it. Only linear algebra made me doubt. , Because its various symbols and operating rules are too abstract and weird, and they do not correspond to life experience at all. Therefore, I really want to thank linear algebra, which inspired me to think about the nature of a mathematics subject. In fact, not only students, but also many mathematics teachers are not clear about what linear algebra is and what its use is, not only in China, but also in foreign countries. Meng Yan in China has written "Understanding the Matrix", and Professor Sheldon Axler in foreign countries has written "Linear algebra should be learned like this", but it has not yet fundamentally explained the ins and outs of linear algebra. For myself, I didn't learn linear algebra when I was in college, but later understood it from a programming perspective. Many people say that mathematics can help programming, but I happened to turn it around. The understanding of programs helped me understand mathematics.
There are general-purpose languages ​​such as assembly, C++/C++, Java, Python, and DSLs such as Makefile, CSS, and SQL in computers. Are these languages ​​an objective natural law or a man-made design?
Why ask such a seemingly stupid question? Because its answer is obvious, everyone's understanding of the programming language used every day must be better than abstract linear algebra. Obviously, although programming languages ​​contain inherent logic, they are essentially artificial designs. The commonality of all programming languages ​​is that a set of models is established, a set of grammars are defined, and each grammar is mapped to specific semantics. The programmer and the language implementer abide by the language contract: the programmer guarantees that the code conforms to the grammar of the language, and the compiler/interpreter guarantees that the result of the code execution conforms to the corresponding semantics of the grammar. For example, C++ stipulates that the new A() syntax is used to construct object A on the heap. If you write C++ in this way, you must ensure the corresponding execution effect, allocate memory on the heap and call the constructor of A, otherwise the compiler violates the language contract.
From an application point of view, can we regard linear algebra as a programming language? The answer is yes, we can use the language contract as a standard to try. Suppose you have an image and you want to rotate it 60 degrees and stretch it by 2 times along the x-axis; linear algebra tells you, "OK! You construct a matrix according to my grammar, and then multiply yours according to the matrix multiplication rules. Image, I guarantee the result is what you want".
In fact, linear algebra is very similar to a DSL such as SQL. Here are some analogies:
Model and semantics: SQL builds a relational model based on low-level languages. The core semantics are relations and relational operations; linear algebra builds a vector model based on elementary mathematics, and the core semantics are vectors and linear transformations.
Syntax: SQL defines the corresponding syntax for each semantic, such as select, where, join, etc.; linear algebra also defines the corresponding syntax for semantic concepts such as vectors, matrices, and matrix multiplication
Compilation/Interpretation: SQL can be compiled/interpreted as C language; the concepts and operation rules of linear algebra can be explained by elementary mathematical knowledge
Realization: We can perform SQL programming on relational databases such as MySQL and Oracle; we can also perform linear algebra programming on mathematical software such as MATLAB and Mathematica
Therefore, from an application point of view, linear algebra is a domain-specific language (DSL) designed by humans, which establishes a set of models and completes the mapping of syntax and semantics through symbol systems. In fact, the grammar and semantics of vectors, matrices, and operation rules are all artificial designs. This is the same as various concepts in a language. It is a kind of creation, but the premise is that the language contract must be satisfied.
Why is there linear algebra?
Some people may be worried about treating linear algebra as a DSL. I will give you a matrix, and you will rotate my graph by 60 degrees and stretch it by 2 times along the x-axis. I always feel uneasy, I don’t even know you. How to do the "bottom"! In fact, this is like some programmers who are not pragmatic with high-level languages, thinking that the bottom layer is the essence of the program, and always want to know what this sentence is compiled into assembly? How much memory is allocated for that operation? Others can take down a webpage by directly typing a wget command in the Shell. He has to spend dozens of minutes in C language to write a bunch of code to be practical. In fact, the so-called bottom and top are just a habitual term, not who is more essential than others. Program compilation and interpretation are essentially semantic mappings between different models. Normally, high-level languages ​​are mapped to low-level languages, but the direction can also be reversed. Fabrice Bellard wrote a virtual machine in JavaScript and ran Linux on the JavaScript virtual machine. This is to map the machine model to the JavaScript model.
The establishment of a new model definitely depends on the existing model, but this is a means of modeling rather than an end. The purpose of any new model is to analyze and solve a certain type of problem more simply. When linear algebra was established, its various concepts and operating rules depended on the knowledge of elementary mathematics, but once this level of abstract model was established, we should be accustomed to directly using high-level abstract models to analyze and solve problems.
Speaking of linear algebra is to analyze and solve problems more easily than elementary mathematics, let's actually experience its benefits through an example:
Given the vertices (x1, y1), (x2, y2), (x3, y3) of the triangle, find the area of ​​the triangle.
The most famous formula for calculating the area of ​​a triangle in elementary mathematics is area = 1/2 * base * height. When a triangle has a side that happens to be on the coordinate axis, we can easily calculate its area. But, what if we rotate the coordinate axis for the same triangle so that its side is not on the coordinate axis? Can we still get its base and height? The answer is definitely yes, but it is obviously complicated, and there are many situations to discuss separately.
On the contrary, if we use linear algebra knowledge to solve this problem, it is very easy. In linear algebra, the cross product of two vectors a and b (Cross Product) is a vector whose direction is perpendicular to a and b, and its size is equal to the area of ​​the parallelogram formed by a and b:
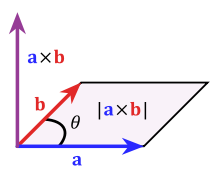
We can treat the sides of a triangle as vectors, so the area of ​​a triangle is equal to the cross product of the two side vectors divided by the absolute value of two:
area = abs(1/2 * cross_product((x2-x1, y2-y1), (x3-x1, y3-y1)))
Note: abs means the absolute value, cross_product means the cross product of two vectors.
Such a difficult problem in elementary mathematics can be solved in an instant in linear algebra! Some people may say that you do it directly based on the cross product. Of course it is simple, but isn't the cross product itself quite complicated? Do you try to expand it? Yes, the role of the model is to hide part of the complexity in the model, so that the user of the model can solve the problem more simply. Someone once questioned that C++ is too complicated, and Bjarne Stroustrup, the father of C++, replied:
Complexity will go somewhere: if not the language then the application code.
In a specific environment, the complexity of the problem is determined by its nature. C++ incorporates part of the complexity into the language and standard library, with the goal of making the application simpler. Of course, not all occasions C++ makes the problem easier, but in principle, the complexity of C++ makes sense. In addition to C++, various languages ​​and frameworks such as Java, SQL, CSS, etc. can't be better. Imagine how complicated it is to do data storage and management by yourself if you don't use a database! In this way, it is not difficult for us to understand why linear algebra defines a strange operation such as cross product. It is the same as C++ incorporating many commonly used algorithms and containers into STL. Similarly, you can even define the operations you want in linear algebra for reuse. Therefore, mathematics is not rigid at all, it is as lively as a program, and you can manage it freely when you understand its ins and outs. Having said that, we will answer a very common doubt by the way:
The dot product, cross product, and matrix operations of linear algebra are very strange. Why do we define these operations? Why are their definitions like this?
In fact, like program reuse, linear algebra defines dot product, cross product and matrix operations because they are widely used and have great reuse value, which can be used as the basis for our analysis and problem solving. For example, if many problems involve the projection of one vector to another vector or the angle between two vectors, then we will consider specifically defining the dot product (Dot Product) operation:
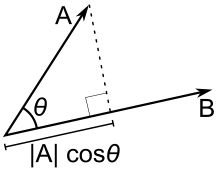
The concept of dot product belongs to design, and there is room for creativity; once the design is finalized, the specific formula cannot be used at will. It must be logical to ensure the correctness of its mapping to the elementary mathematical model. This is like a high-level language that can define many concepts, such as high-order functions, closures, etc., but it must ensure that the effects of execution when mapped to the underlying implementation conform to its defined specifications.
What is so good about linear algebra?
As mentioned above, linear algebra is a high-level abstract model. We can learn its syntax and semantics by learning a programming language, but this understanding is not only for linear algebra, it is common to every subject of mathematics Yes, some people may have questions
Calculus and probability theory are also high-level abstractions, so what are the characteristics of high-level abstractions like linear algebra?
This asks the fundamental, the core of linear algebra: the vector model. The coordinate system that we learn in elementary mathematics belongs to the analytical model proposed by Descartes. This model is very useful, but it also has great shortcomings. The coordinate system is a virtual reference system added artificially, but the problems we have to solve, such as seeking area, graphics rotation, stretching and other applications are not related to the coordinate system. Establishing a virtual coordinate system often does not help solve the problem. This is the example of the area of ​​a triangle just now.
The vector model overcomes the shortcomings of the analytical model very well. If the analytical model represents a certain "absolute" world view, then the vector model represents a certain "relative" world view. I recommend combining the vector model and the analytical model. Seen as two opposite models.
The concept of vector and scalar is defined in the vector model. A vector has size and direction, satisfying the linear combination rule; a scalar is a quantity with only size and no direction (note: another more profound definition of scalar is a quantity that remains constant in coordinate transformation). One of the advantages of the vector model is that its coordinate system is irrelevant, which is relativity. When defining the vector and operation rules, it puts aside the constraints of the coordinate system from the beginning. No matter how you rotate the coordinate axis, I can adapt to it. , Vector linear combination, inner product, cross product, linear transformation and other operations are all coordinate system-independent. Note that the so-called independence of the coordinate system does not mean that there is no coordinate system, but it does exist. The vertices of the triangle example just now are represented by coordinates, but different coordinate systems will not affect the problem when solving the problem. To use an analogy, Java claims to be platform-agnostic. It does not mean that Java is a castle in the air, but that when you use Java to program, whether the underlying is Linux or Windows often has no effect on you.
What are the benefits of the vector model? In addition to the triangle area problem just now is an example, let me give another geometric example below:
Given a point (x0, y0, z0) in a three-dimensional coordinate system and a plane a*x + b*y + c*z + d = 0, find the vertical distance from the point to the plane?
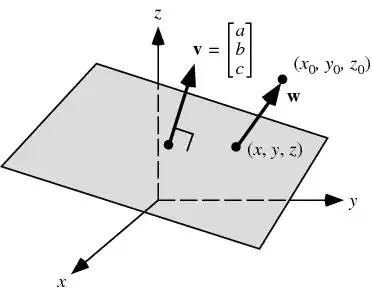
If this problem is to be solved from the perspective of analytic geometry, it is almost too complicated to start, unless it is a special case where the plane happens to pass the coordinate axis, but if it is considered from the vector model, it is very simple: according to the plane equation, the normal vector of the plane ( Normal Vector) is v=(a, b, c), set the vector from any point (x, y, z) to (x0, y0, z0) on the plane to be w, then through the inner product dot_product(w, v) Calculate the projection vector p from w to v, and its size is the vertical distance from (x0, y0, z0) to the plane a*x + b*y + c*z + d = 0. The basic concepts of the vector model are used here: normal vector, projection vector, inner product, and the whole problem solving process is simple and clear.
Let me leave you a similar exercise below (friends who are familiar with machine learning may find that this is the application of linear algebra in linear classification):
Given two points (a1, a2, ... an), (b1, b2, ... bn) in n-dimensional space and a hyperplane c1*x1 + c2*x2 ... + cn*xn + d = 0, please determine whether the two points are on the same side or on the opposite side of the hyperplane?
Leaving the vector, we are going to call out another protagonist of linear algebra: Matrix.
Linear algebra defines the multiplication of matrices and vectors, matrices and matrices. The operation rules are very complicated, and it is not clear what it is used for. Many beginners can't understand it well. It can be said that matrices are the obstacle to learning linear algebra. When encountering complex things, it is often necessary to avoid getting into the details first and grasp it as a whole. In fact, from a program point of view, no matter how strange the form is, it is nothing more than a kind of grammar, and the grammar must correspond to the semantics, so the key to understanding the matrix is ​​to understand its semantics. The semantics of a matrix is ​​more than one. There are different semantics in different environments, and different interpretations in the same environment. The most common ones include: 1) Representing a linear transformation; 2) Representing a collection of column vectors or row vectors ; 3) Represents a collection of sub-matrices.
Matrix as a whole corresponds to linear transformation semantics: multiply matrix A by a vector v to get w, and matrix A represents the linear transformation from v to w. For example, if you want to rotate the vector v0 60 degrees counterclockwise to get v', just use the Rotation Matrix to multiply v0.
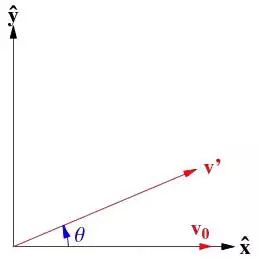
In addition to rotation transformation, stretching transformation is also a common transformation. For example, we can stretch a vector along the x-axis by a stretch matrix by 2 times (please try to give the form of the stretch matrix by yourself). More importantly, matrix multiplication has a good property: it satisfies the combination rate. This means that linear transformations can be superimposed. For example, we can multiply the matrix M "rotated by 60 degrees counterclockwise" and the matrix N "stretched by 2 times along the x axis" to get a new matrix T to represent "Rotate 60 degrees counterclockwise and stretch 2 times along the x-axis." Isn't it a lot like superimposing multiple commands through pipelines in our Shell?
The above focuses on the independence of the coordinate system of the vector model. In addition, another advantage of the vector model is: linearity, so it can be used to express linear relationships. Let's look at an example of a familiar Fibonacci sequence:
The Fibonacci sequence is defined as: f(n) = f(n-1) + f(n-2), f(0) = 0, f(1) = 1; question: input n, please give f(n The time complexity of) does not exceed O(logn) algorithm.
First, we construct two vectors v1 = (f(n+1), f(n)) and v2 = (f(n+2), f(n+1)). According to the nature of the Fibonacci sequence, we can get from The recursive transformation matrix from v1 to v2:
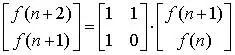
And further get:
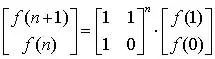
In this way, the linear recurrence problem is transformed into the classic problem of the n-th power of the matrix, which can be solved in O(log n) time complexity. In addition to linear recurrence series, the famous n-ary linear equations in elementary mathematics can also be transformed into matrix and vector multiplication forms to be solved more easily. This example is to illustrate that any system that satisfies a linear relationship is a vector model. We can often convert it into linear algebra to get a simple and efficient solution.
In short, my experience is that the vector model is the core of the entire linear algebra, and the concept, nature, relationship, and transformation of vectors are the key to mastering and using linear algebra.
to sum up
This article puts forward a point of view: From an application point of view, we can regard linear algebra as a programming language in a specific field. Linear algebra establishes a vector model on the basis of elementary mathematics, defines a set of syntax and semantics, and conforms to the language contract of programming languages. The vector model has the independence and linearity of the coordinate system. It is the core of the entire linear algebra and is the best model for solving linear space problems.
Stand Table Fan ,14 Inch Oscillating Table Fan,Pedestal Table Fan,Height Adjustable Table Fan
Foshan Shunde Josintech Electrical Appliance Technology Co.,Ltd , https://www.josintech.com